Introduction
Political debates over the past two decades have placed the issues of income and wealth inequality front and center. While these debates tend to focus on the causes and consequences of inequality, they often presuppose that inequality has taken off dramatically in recent years. But has inequality, in fact, increased?
As it turns out, answering this question is more difficult than it may appear. Questions such as: “inequality of what?,” “over what period?,” “measured how?” may seem like trivia designed to distract from the broader issue, but they are in fact all choices that an analyst seeking to study this question must address. In this post, we show that economic inequality in the US is sensitive to such measurement issues and, depending on the approach chosen, one can marshal evidence to show that inequality has increased, stayed the same, or even decreased over time. These results speak to both the danger of using single measures to characterize entire distributions, as well as to the precise dynamics of changing inequality in the US.
To approach this issue, we use publicly available data from Kuhn, Schularick, and Steins (2020) “Income and Wealth Inequality in America, 1949-2016”. This paper draws from the Survey of Consumer Finances to construct a panel of income and wealth dynamics over the past 70 years. We construct time series of inequality over different variables, different time periods, and using different measures, and show that these choices have meaningful effects.
Inequality of what?
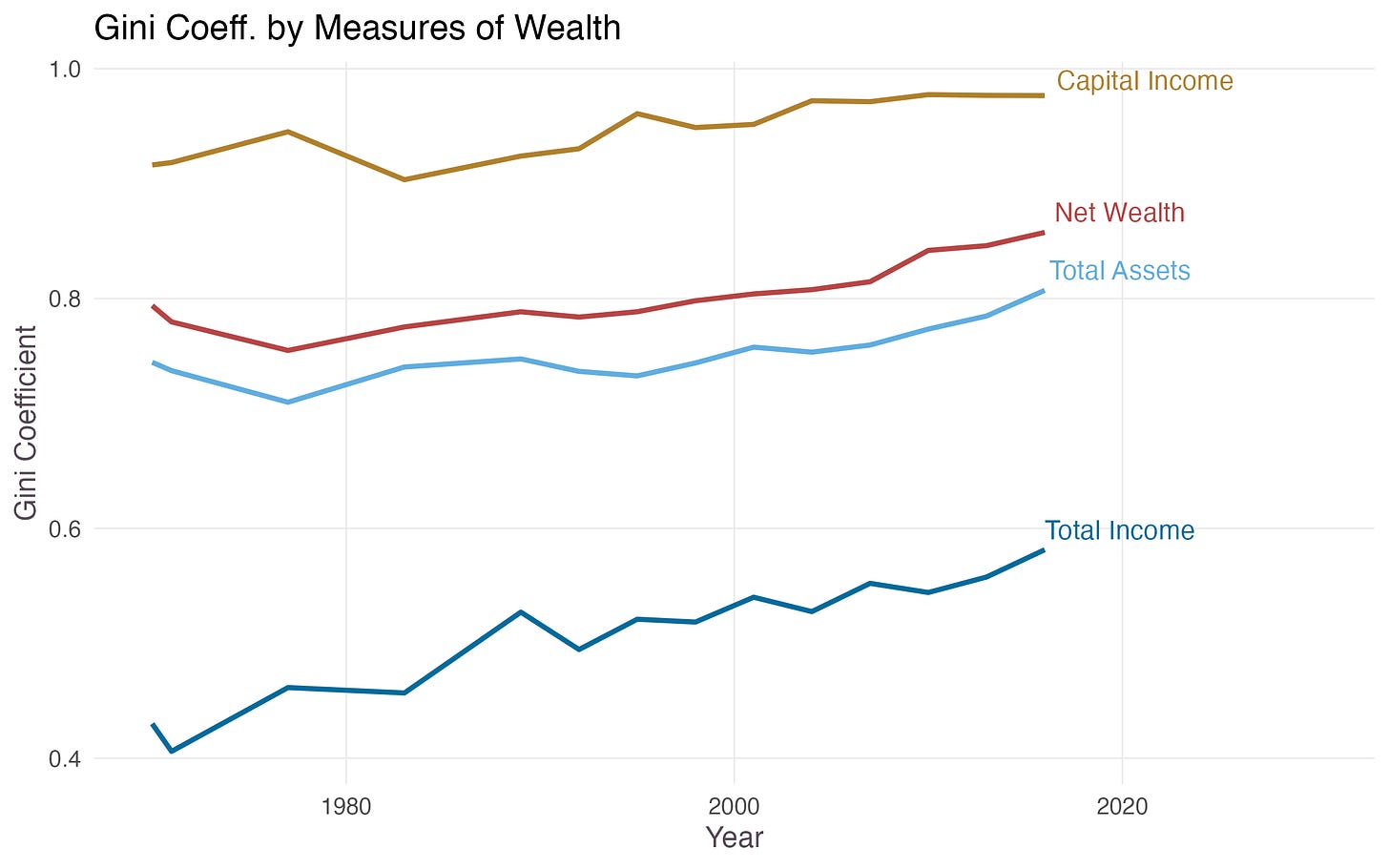
A first issue in measuring inequality involves the choice of variable we which to measure. Frequently, “wealth”, “income”, and “consumption” are used interchangeably under a broad notion of economic inequality, but this type of language can mask large and important differences, both statistically and economically. To see this, consider the Gini coefficient taken over four different measures of economic wellbeing from the data: total income, capital income, total assets, and net wealth.
While all measures seem to have increased since 1970, there is substantial heterogeneity both in level and in changes. First, in levels, we notice that capital income reflects a far higher degree of inequality that any other measure. This is perhaps not so surprising, given that capital income reflects interest, dividends, rents, and capital gains in markets in which many Americans never participate. Also, unlike variables like labor income, capital income can take on negative values (e.g. from negative capital gains), which even further skews the distribution.
But even measures like net wealth and total income have vastly different degrees of inequality; at times, the distribution of net wealth was almost twice as unequal as total income. And while inequality in total assets, capital income, and net wealth, have increased somewhat gradually, inequality of total income has risen by more than 30% over the past 50 years. There are even periods, such as during the 1970s, when inequality in total income and net wealth moved in opposite directions. Questions like “to what extent is America unequal” and “to what extent has this inequality increased” thus depend a lot on what type of inequality we are talking about.
The figure above highlights the importance of being precise about the notion of inequality one wishes to measure. Net wealth — defined as a household’s assets less its debt — speaks to accumulated assets, such as stocks, bonds, and the equity share of housing. Total income, on the other hand, speaks to the flow of income a household earns each year. While income furnishes households with the ability to accumulate net wealth, they clearly do not move in lockstep, with differences attributed to things like equity and house prices. This is a key argument of Kuhn, Schularick, and Steins (2020) that we will revisit in the conclusion.
Over what period?
A second issue involves the choice of sample period. The point here is more about presentation of data than about statistical analysis itself, but given the importance of data visualization to economic arguments, we illustrate how sensitive statements about the direction of inequality — let alone the magnitude — can be to the sample period analyzed.
For all four economic measures above, we consider the absolute change in the Gini coefficient over different sample time periods. We compare it to the unconditional change over 1970-2016:
As we can see, while all measures of inequality have increased since 1970 (red bars), they depend a lot on the sample period. Some periods see increases in inequality across the board (2007-2016) while other periods reflect a more complicated story (1970-1995). It is easy to see how this heterogeneity could be used selectively to make misleading statements. (1) “Wealth inequality declined in the latter third of the 20th century”; (2) “there has been negligible change in capital income inequality since 1995” and (3) “all four measures of income inequality have increased significantly since 1970” are all correct statements one could make using this data, but potentially lend themselves to different narratives.
There are three takeaways from this exercise. The first is a narrow point about data visualization: using bar graphs for time series data may mask a lot of important information regarding interim dynamics, particularly when the bars aggregate data over long intervals. A time-series line of Gini coefficients for example, as in Fig. 1, would make it much easier for a reader to analyze any specific subperiod they want. The second is a more nuanced point about choosing sample periods: because trends can be so sensitive to the choice of start (and end) date, it is best to use data-driven approaches to pick the start year (i.e. when data is first available, or when a “regime” first started) rather than ex post selecting a starting year to validate a narrative. In general, if you cannot understand why a specific start and end point are chosen, you should exercise healthy skepticism. Finally, heterogeneity in trends by sample period, and across measures within different sample periods, can speak to underlying features in the economy. That income inequality rose so much in the first half of the sample and wealth/asset inequality rose so much in the second relates in part to the impact of the financial crisis on different measures on inequality.
Measured how?
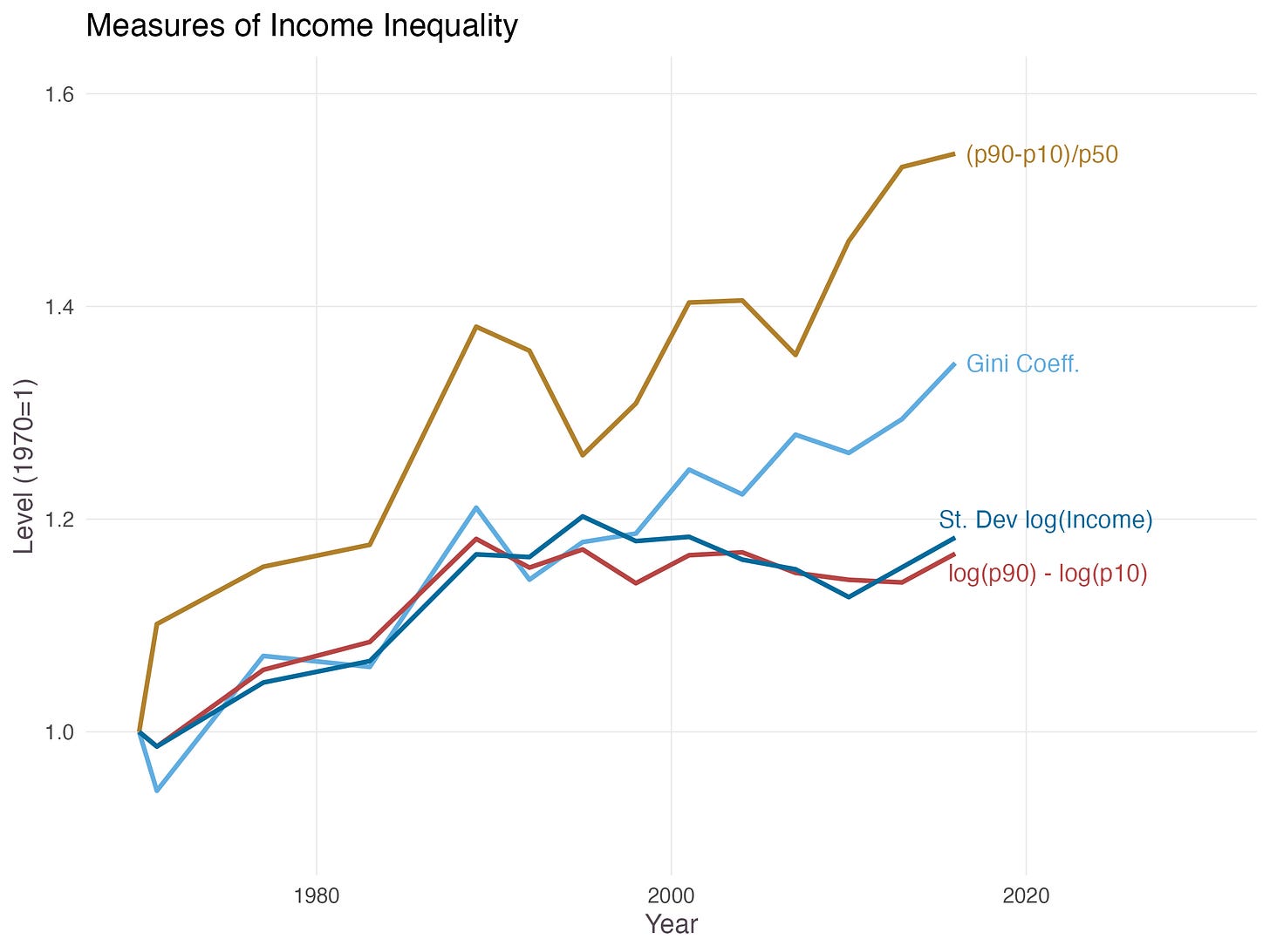
A final issue is the choice of inequality measure itself. Heretofore we have used the Gini coefficient as our measure of inequality, which is likely the most widely used measure of inequality. But this measure can be difficult to understand intuitively, and is by no means the only measure of inequality out there. Another common measure looks at some dispersion in the quantiles of the distribution; for example, the income of the 90th percentile household (”p90”) minus the income of the 10th percentile household (”p10”). If inequality increases — say, the top 20% of households see disproportionate increases in income — then a p90-p10 measure will increase as well. To avoid rising incomes mechanically raising p90-p10 (e.g. due to economic growth), we might, as a last step, “scale” a p90-p10 variable, by dividing the difference by the median income: (p90-p10)/p50, or consider the (log) of the ratio p90/p10, instead of the raw difference.
In the figure below we plot the time series of these measures, along with a third measure — the standard deviation of log total income — which captures how “spread out” the income distribution is from its mean (intuitively: a more dispersed income distribution, i.e. with richer and poorer people, will have a higher standard deviation). We also include a normalized Gini coefficient (also scaled so that 1970=1), though since this type of normalization may not be as appropriate for Gini coefficients, we caution against reading too deeply into it.
Once more, we see heterogeneity in the dynamics: the (p90-p10)/p50 has increased steadily across the sample, while measures like log(p90)-log(p10) and the standard deviation of log income have remained steady since the 1990’s (or even decreased!).
As we have emphasized, studying the difference between these series can shed light on what is happening to the US income distribution. That inequality in (p90-p10)/p50 rises so much faster than inequality in log(p90)-log(p10) suggests that perhaps dividing by the median income is not such an innocuous scaling method. If the median income has fallen relative to the (right) tail of the income distribution, then (p90-p10)/p50 will increase, with little change in log(p90)-log(p10). Second, the Gini coefficient has increased far more than both log(p90)-log(p10) and the standard deviation of log income. This suggests that a large part of the change in the income distribution may be in the right tail, i.e. households with income above the 90th percentile. If the top 1% or 0.01% see disproportionate increases in income, this will show up in the Gini coefficient but will have no effect on p90 or p10, and may only have a slight effect on the standard deviation of log income (which assigns small weights to the tail). In other words, not only are these differences interesting insofar as they speak to the difficulties in measurement, but they also uncover some crucial features about the time series of income: (1) stagnant median income post 1990s (relative to the distribution) and (2) rising inequality driven by increases in the far right tail (>90th percentile).
The Full Distribution
Given the wide variety of inequality measures, how should an analyst proceed? One solution is simply to be precise about the notion and measure of inequality: for example, if one is concerned about the ability of the very rich to command resources, they might choose something like the “net wealth share of the 1% since 1990.” In other words, rather than speaking to all measures/notions of inequality, they choose one appropriate for their purposes, with well defined meaning and construction. However, it is important to note that the rationale for this choice must come from a model or specific question; nothing from the data tells us the correct statistic to use.
A second alternative is just to consider the full distribution, rather than any summary statistic. While visualizing/communicating full distributions can be difficult, we show one way to do it below with a ridgeline (or “joy”) plot. For a set of years 1949-2016, we plot the distribution of log total income (dropping zeros and negative observations), along with lines denoting the 1st, 10th, 50th (median), 90th, and 99th percentiles.
Seeing the full distribution provides insights that individual statistics may miss. There has been steady, but very small progress in p10 (and p50 as well). But this is dwarfed by the rise in the 90th percentile, and indeed the far right tail overall.
The full distribution clarifies some of the findings above that seemed intuitively inconsistent on a first pass. From the 1950s to the 1990s, the dispersion in total income did increase, but from 1990 to today, the dispersion increase has been minimal. However, the right tail is getting somewhat fatter, as we can see by the marked rightward shift of the 99th percentile line. This helps explain why the Gini coefficient for this distribution has been increasing: the share of total income held by the top x% has been increasing, and when we account for the fact that the above figure is in logs, not levels, it becomes apparent that the increase must be quite large, regardless of whether we compare to 1990 or 1949. This understanding also explains why the (p90-p10)/p50 ratio has skyrocketed: the 10th and 50th percentiles have seen level gains, but nowhere near the level gains of the 90th percentile.
We can also consider the relevant net wealth distribution:
Again, dropping the non-positive observations understates the level of inequality in net wealth, but even in this conditional distribution we see that the gains for 10th percentile are paltry, the gains for the median moderate, and the gains for the 90th percentile marked. The only reason we don’t see such a pronounced Gini rise in net wealth is because it was already high in 1949.
To see this idea more clearly, we can “unwind” the Gini calculation and look directly at the Lorenz curves, L, which are another means of visualizing an entire distribution, and which say “The share of the total [total income or net wealth] held by the bottom q of the population (x-axis) is L(q) (y-axis)”. Under perfect equality (bottom x% of population holds exactly x% of the wealth), the Lorenz curve is a straight line, y=x. As society becomes more unequal, the curve looks more like a “J”, with low holdings in the left tail and high holdings in the right tail. The Lorenz curves relate to Gini coefficients in that the Gini coefficient is simple the amount of area between the perfectly equal curve and the true Lorenz curve for a country.
Below, we plot the Lorenz curve for 3 sample years (1949, 1989, and 2016) across two different economic variables (total income and net wealth). We also show, in purple, the line of total equality:
We can see that the total income curves are much closer to the line of equality at all time periods, but that the shift over time has added a fair amount of area between the line of equality and the Lorenz curve. The change in net wealth curves, on the other hand, have added less area to the gap, but the gap was already large to begin with.
Conclusion
The lesson from this post is that (a) measures of economic inequality do not all move in lockstep and (b) characterizing an entire distribution with a single number can be misleading. Both points imply the importance of precision when describing economic inequality. Statements like “the incomes of the 90th and 10th percentile have seen similar growth post-1995, but the top 1% income has grown disproportionately” are not only more informative than broad statements about “increasing inequality,” but also are less susceptible to criticism.
We conclude this blog post with some additional thoughts on measuring inequality.
Measuring Wealth: The discussion here took the different variables as given (i.e. correct), and analyzed differences among them. But a large academic debate disagrees about the proper construction of a variable like “wealth”. Typically the way we construct wealth is to aggregate assets, and add “capitalized” income streams —i.e. we figure out a way to discount the income stream to assign a present value to it. What discount rate to use (and does it differ by rich or poor?), how much of inequality is due to secular changes in discount rates, and what income streams to use (e.g. government transfers, social security, human capital, etc.) is a matter of significant academic debate. See Smith, Zidar, and Zwick (2023); Saez and Zucman (2020); Catherine, Miller, and Sarin (2022); and Greenwald, Leombroni, Lustig, and van Nieuwerbergh (2021) for recent discussion of some these issues.
Statistical Choices: At the other end of the spectrum from questions of what constitutes wealth are very small statistical questions that arose in this analysis: How do you treat 0 or negative wealth (a problem when using a logarithm)? If you want to compare two Gini coefficient series — say one on wealth, one on income — should you plot cumulative changes or relative changes? (As it turns out, which you plot matters a lot). Do we look at inequality among individuals or among households? These are, in a sense, minor econometric issues, but they can introduce additional sources of variation in measuring inequality.
Sources of Inequality: This analysis has only lightly discussed the reasons for rising inequality, focusing more on issues on inequality measurement and presentation. An excellent treatment of why different measures have different dynamics (and over different time periods) can be found in the original Kuhn, Schularick, and Steins (2020) paper from which we borrow the data. A main point from that paper is that, because wealthy households hold a disproportionate share of financial assets, asset price movements have first-order implications for wealth distributions in ways that are decoupled from changes in income or changes in non-financial assets (like housing). This explains in large part the different dynamics pre- and post-financial crisis: stock prices recovered more quickly than housing prices after 2007, leading to significant increases in net wealth inequality, but comparatively smaller changes in income inequality.